Leggi di Keplero
Fino al 1543 il modello più importante per l'universo, a quel tempo limitato al Sistema Solare, era quello tolemaico, che poneva la Terra al centro, gli altri pianeti, incluso il Sole, in rotazione intorno ad essa e sullo sfondo
le stelle fisse.
Il primo colpo a questa visione dello stato di cose venne dato da Copernico proprio nel 1543 con la descrizione del sistema copernicano o eliocentrico su De revolutionibus orbium coelestium, pubblicato
il 24 maggio, giorno della morte dello stesso Copernico.
Grazie al lavoro di Copernico (probabilmente basato anche sul lavoro di Giovanni Battista Amici), altri astronomi e scienziati proposero nuove idee sul funzionamento del nostro universo:
tra questi, oltre all'italiano Galileo Galilei, si segnala il tedesco Johannes Kepler, italianizzato in Keplero, che basandosi sulle osservazioni di Tycho Brahe, formulò le sue famose
tre leggi.
Prima legge di Keplero
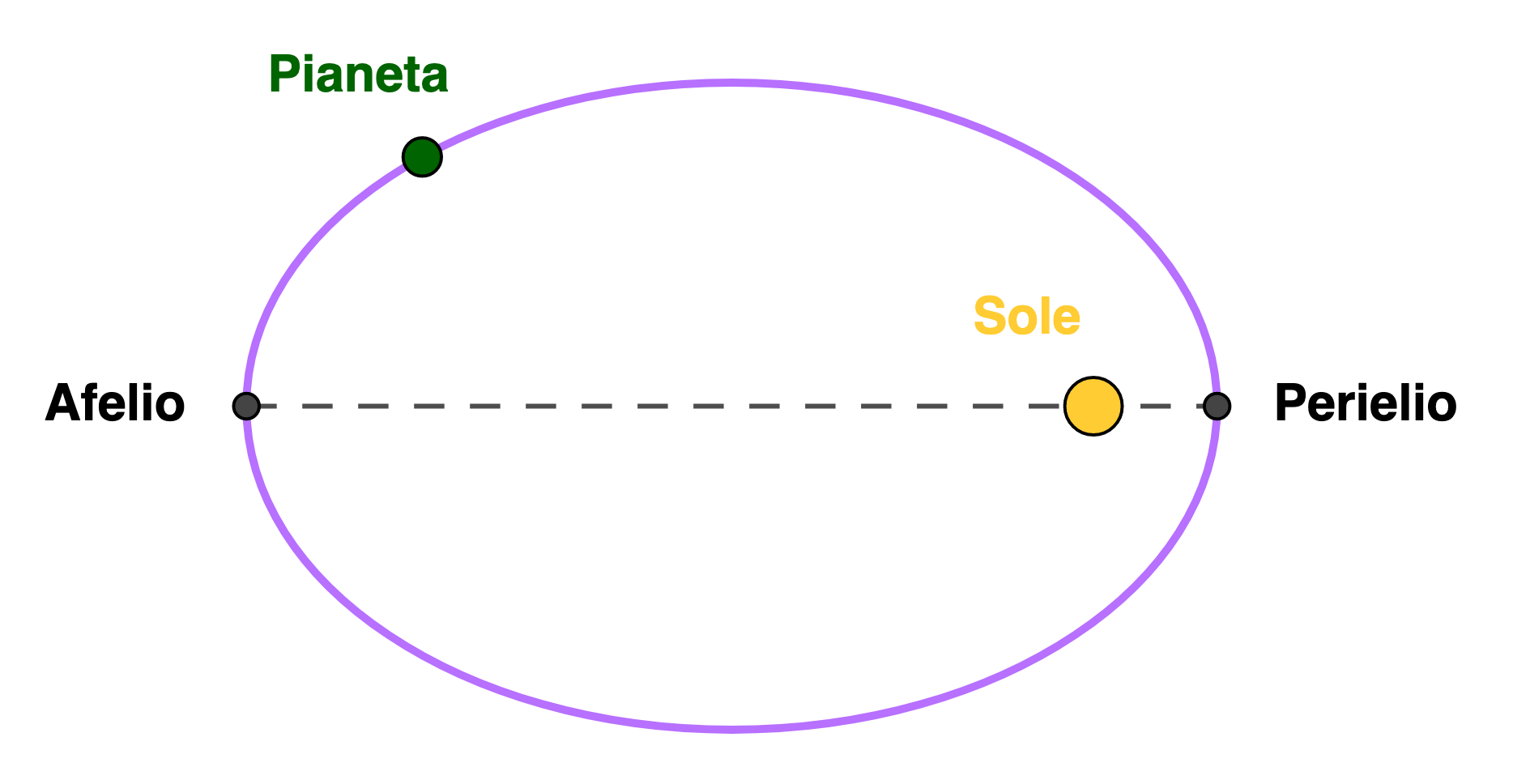
Tutti i pianeti si muovono su orbite ellittiche con il Sole in uno dei fuochi.
Ne consegue che la distanza dei pianeti dal Sole non è costante, ma è minima al perielio e massima all'afelio.
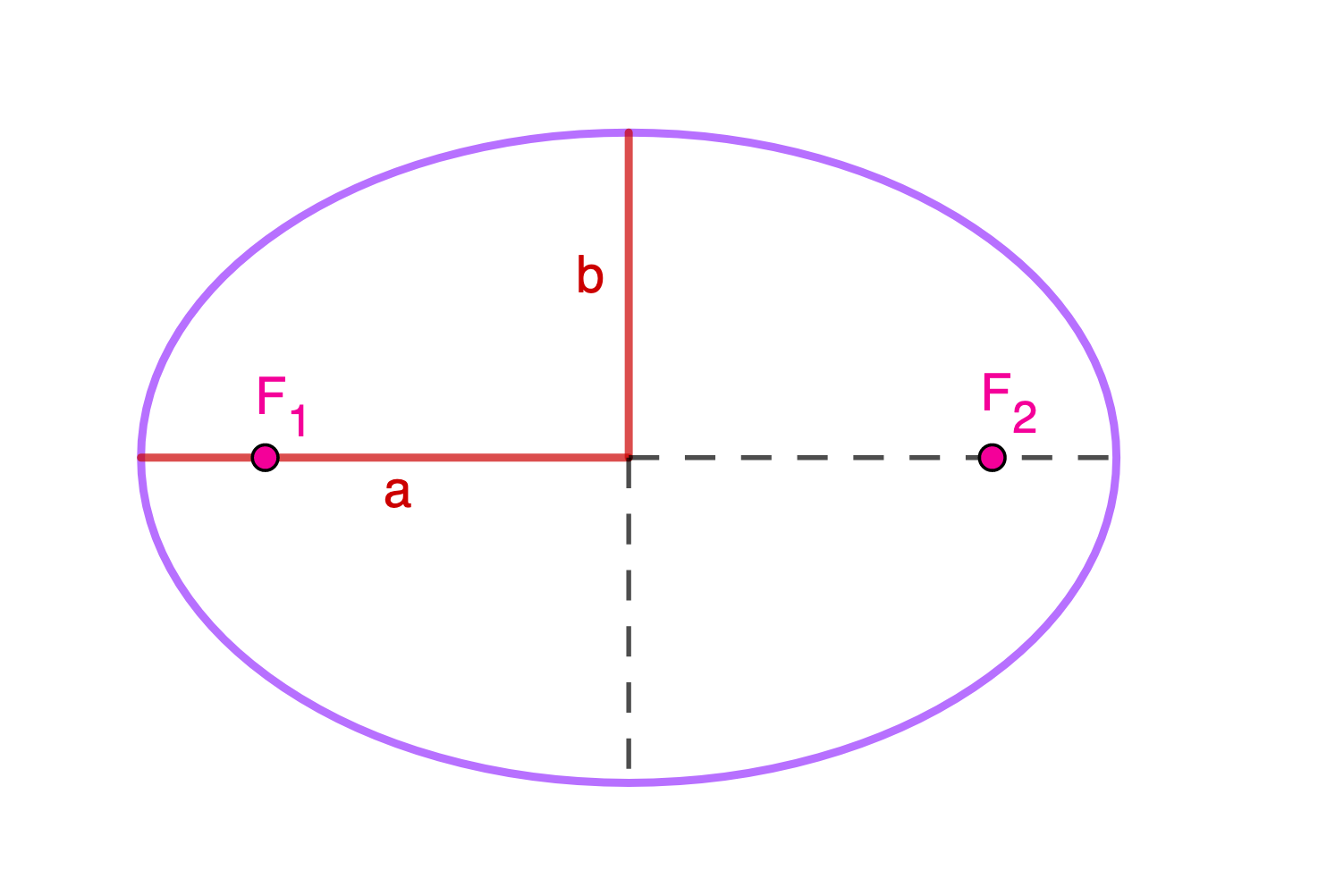
L'ellisse è una sezione conica e può essere definita come il luogo dei punti del piano per i quali la somma delle distanze da due punti fissi, detti fuochi (F1 e F2), rimane costante.
Il segmento "a" è detto semiasse maggiore, "b" semiasse minore.
L'eccentricità si calcola dalla formula: \( e = \sqrt{1- \frac{b^2}{a^2}} \)
Le orbite dei pianeti sono ellissi con una eccentricità molto bassa (eTerra= 0.0167), ovvero molto simili a circonferenze. Asteroidi e comete invece hanno orbite con eccentricità maggiori.
Seconda legge di Keplero
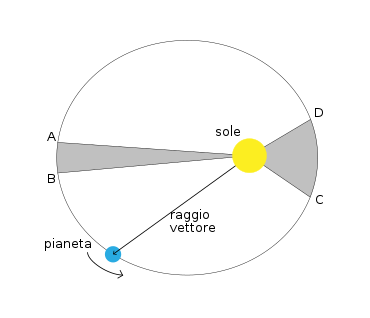
Il raggio vettore che unisce un pianeta al Sole spazza aree uguali in tempi uguali.
Ne consegue che la velocità di un pianeta lungo la sua orbita non è costante, ma è maggiore al perielio e minore all’afelio.
Dalla Seconda Legge si può ricavare la seguente formula: \(v_A \cdot D_A = v_P \cdot D_P \) dove \( v_A \) è la velocità di un corpo all’afelio, \( v_P \) la sua velocità al perielio, \( D_A = a (1+e) \) la distanza dal Sole all'afelio e \( D_P = a (1-e) \) la distanza dal Sole al perielio.
Terza legge di Keplero
Il quadrato del periodo di rivoluzione (T) di un pianeta è direttamente proporzionale al cubo del semiasse maggiore dell'orbita.
Ovvero \( \frac{T^2}{a^3} = k = costante \). Ne consegue che maggiore è la distanza dal Sole, maggiore è il tempo necessario per completare una rivoluzione.
Dati due corpi qualsiasi in orbita intorno al Sole vale la relazione: \( \frac{a_1^3}{a_2^3} = \frac{T_1^2}{T_2^2} \)
Quindi la terza legge fornisce un modello in scala del Sistema Solare, nota una qualsiasi distanza e i tempi di rivoluzione, si possono ricavare tutte le altre.
Per i pianeti in orbita intorno al Sole, il valore della "costante" è: \( k=\frac{4 \pi^2}{(M_{Sole}+M_{pianeta})G} \) (dove G = 6.67 · 10-11 m3kg-1s-2 è la Costante di Gravitazione Universale), ma poiché la massa del Sole è molto maggiore di qualsiasi corpo del Sistema Solare, vale l’approssimazione: \( k=\frac{4 \pi^2}{M_{Sole}G} \) e la Terza Legge di Keplero assume la forma: \( T^2 = \frac{4 \pi^2}{M_{Sole}G} a^3 \).
In particolare, esprimendo il semiasse maggiore dell’orbita di un corpo in UA (Unità Astronomica = semiasse maggiore dell’orbita della Terra = 149.6 · 106 km) e il suo periodo di rivoluzione in anni, la formula precedente si semplifica in: \( a^3 (UA) = T^2 (anni) \).
Se invece consideriamo il moto di un corpo di massa trascurabile attorno a un pianeta, vale l’approssimazione: \( k=\frac{4 \pi^2}{M_{pianeta}G} \) e la Terza Legge di Keplero assume la forma: \( T^2 = \frac{4 \pi^2}{M_{pianeta}G} a^3 \)
Infine, nel caso di corpi con massa (M e m) non molto diversa tra loro, la Terza Legge di Keplero va utilizzata nella cosiddetta forma generalizzata: \( T^2 = \frac{4 \pi^2}{(M+m)G} a^3 \)