Lezioni ed esercizi categoria Junior 2

Il diagramma che ha in ascissa (asse orizzontale) la temperatura e in ordinata (asse verticale) la luminosità delle stelle si chiama diagramma di Hertzsprung-Russell, (prende nome dai due astronomi che l'hanno ideato e viene spesso abbreviato in diagramma HR).

La temperatura riportata in ascissa è decrescente (si va cioè da valori maggiori a sinistra, verso valori minori a destra). In ordinata al posto della luminosità viene spesso riportata la Magnitudine Assoluta delle stelle. In ascissa al posto della temperatura si può riportare il tipo spettrale, oppure il cosiddetto “indice di colore” (la differenza tra le magnitudini della stella misurate in due diverse regioni dello spettro elettromagnetico), che è una quantità direttamente legata alla temperatura. Queste rappresentazioni sono del tutto equivalenti.

Inserendo nel diagramma HR i dati di luminosità (o magnitudine assoluta) e temperatura di numerose stelle, si nota subito che il diagramma non risulta uniformemente popolato. La maggior parte delle stelle (circa il 90%) si posizionano lungo una diagonale che va dall'angolo in alto a sinistra (stelle molto luminose e calde) all’angolo in basso a destra (stelle poco luminose e fredde). Questa diagonale è chiamata Sequenza Principale. Dalla teoria dell’evoluzione stellare sappiamo che le stelle occupano questa regione nel diagramma durante la fase di fusione nucleare dell'idrogeno in elio, che è la fase più lunga e stabile della loro vita. Nel diagramma HR il Sole è una stella di sequenza principale.
In basso a sinistra del diagramma si trova la sequenza delle nane bianche, mentre sopra la sequenza principale, verso destra, troviamo le stelle nella fase di gigante rossa o supergigante. 

Durante il suo ciclo vitale, una stella cambia temperatura e luminosità. Man mano che una stella invecchia (nel gergo degli astrofisici si evolve) la sua posizione sul diagramma HR cambia. Stelle con massa diversa si sposteranno sul diagramma HR seguendo percorsi diversi e in tempi diversi. La corretta previsione del rapporto del numero di stelle nelle varie regioni del diagramma HR è uno dei risultati più importanti della teoria dell’evoluzione stellare.

Analizzando il diagramma HR notiamo che a parità di temperatura della fotosfera le stelle possono avere luminosità diverse. Questo ha portato a una classificazione spettrale più accurata “bidimensionale” dovuta in origine agli astronomi Morgan e Keenan. Oggi a ogni tipo spettrale si associa una “Classe di luminosità” che, a parità di temperatura, è un indice del raggio della stella. Le classi di luminosità attualmente utilizzate sono:

0 = Ipergiganti

I = supergiganti

II = Giganti brillanti

III = Giganti

IV = Sub-giganti

V = Nane (o stelle di sequenza principale)

VI = Sub-nane

VII = Nane bianche (anche indicate con la sigla WD)

In questa classificazione il Sole è una stella di tipo G2 V.

Diagramma HR e distanze

Il diagramma HR è costruito a partire da stelle per le quali, oltre la temperatura (o il tipo spettrale o l’indice di colore) è nota la distanza (d). Può tuttavia essere utilizzato per determinare la distanza di una stella di cui sono noti tipo spettrale e classe di luminosità e per la quale è stata misurata la magnitudine apparente (m). Posizionando la stella nel diagramma HR si può ricavare la sua magnitudine assoluta (M) e dalla formula che lega magnitudine assoluta con magnitudine apparente e distanza (M = m + 5 – 5 log d) si può ricavare la distanza in parsec:

\( d = 10^{\frac{m-M+5}{5}} \) 

Infine, di particolare interesse è il diagramma HR di gruppi di stelle quali gli ammassi aperti e globulari. Per gli ammassi, dato che le loro dimensioni sono in generale trascurabili rispetto alla loro distanza, si può sostituire la magnitudine apparente al posto di quella assoluta. Lo studio dei diagrammi HR degli ammassi aperti e globulari è fondamentale per la comprensione dell’evoluzione stellare.

Relazione massa-luminosità

La relazione massa-luminosità è un'equazione che mette in relazione la massa (M) di una stella e la sua luminosità (L):

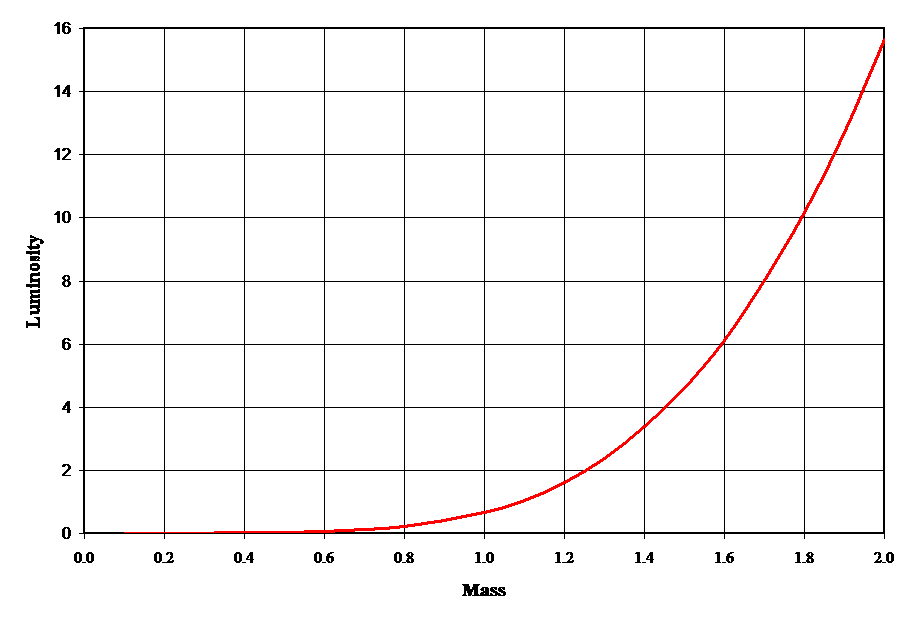
\( \frac{L}{L_{\odot}} = \left( \frac{M}{M_{\odot}} \right)^{\alpha} \)

dove \( L_{\odot} \) e \( M_{\odot} \) sono la luminosità e la massa del Sole e α è un indice che dipende dalla massa della stelle.

Questa equazione empirica viene in genere utilizzata solo per le stelle della sequenza principale, con α = 4 per stelle con massa \( 0.43 M_{\odot} < M < 2 M_{\odot} \) (rappresentata nell'immagine a fianco) e con con α = 3.5 per stelle con massa  \( 2 M_{\odot }< M < 55 M_{\odot} \).

Durata tipica della fase di sequenza principale per stelle di diversa massa

Argomento richiesto solo per la finale

La relazione massa-luminosità può essere usata per determinare il tempo di vita di una stella, poiché esso è proporzionale al rapporto massa/luminosità.

Le stelle, per sopravvivere, devono produrre energia per mantenere l'equilibrio con la forza di gravità che tenderebbe a farle collassare (equilibrio idrostatico). L'energia viene prodotta nel nucleo dalle reazioni nucleari e dopo essere stata trasportata (con vari meccanismi) verso le parti esterne viene infine emessa nello spazio sotto forma di radiazione. Poiché la luminosità equivale all'energia prodotta nell'unità di tempo, in prima approssimazione si può dedurre la durata della vita di una stella stimando l'energia che può produrre durante la sua esistenza e dividendola per la sua luminosità.

Contrariamente a quello che si potrebbe pensare, le stelle di massa maggiore, sebbene dispongano di maggior combustibile nucleare, hanno una vita più breve, perché al crescere della massa l'incremento della luminosità è maggiore di quello della massa stessa. 

Esprimendo la massa di una stella in unità di masse solari, il tempo di permanenza sulla sequenza principale è dato dalla relazione:

\( T_{MS} (anni) = \frac{10 \cdot 10^9}{M^{2.5}} \)

Da questa relazione ricaviamo che il Sole ha un tempo di permanenza sulla sequenza principale di 10 miliardi di anni. Una stella con 50 masse solari resta in sequenza principale meno di 600000 anni, mentre una stella da 0.5 masse solari resta in sequenza principale per quasi 60 miliardi di anni.