Giorno siderale e tempo siderale
Argomento richiesto solo per la finale.
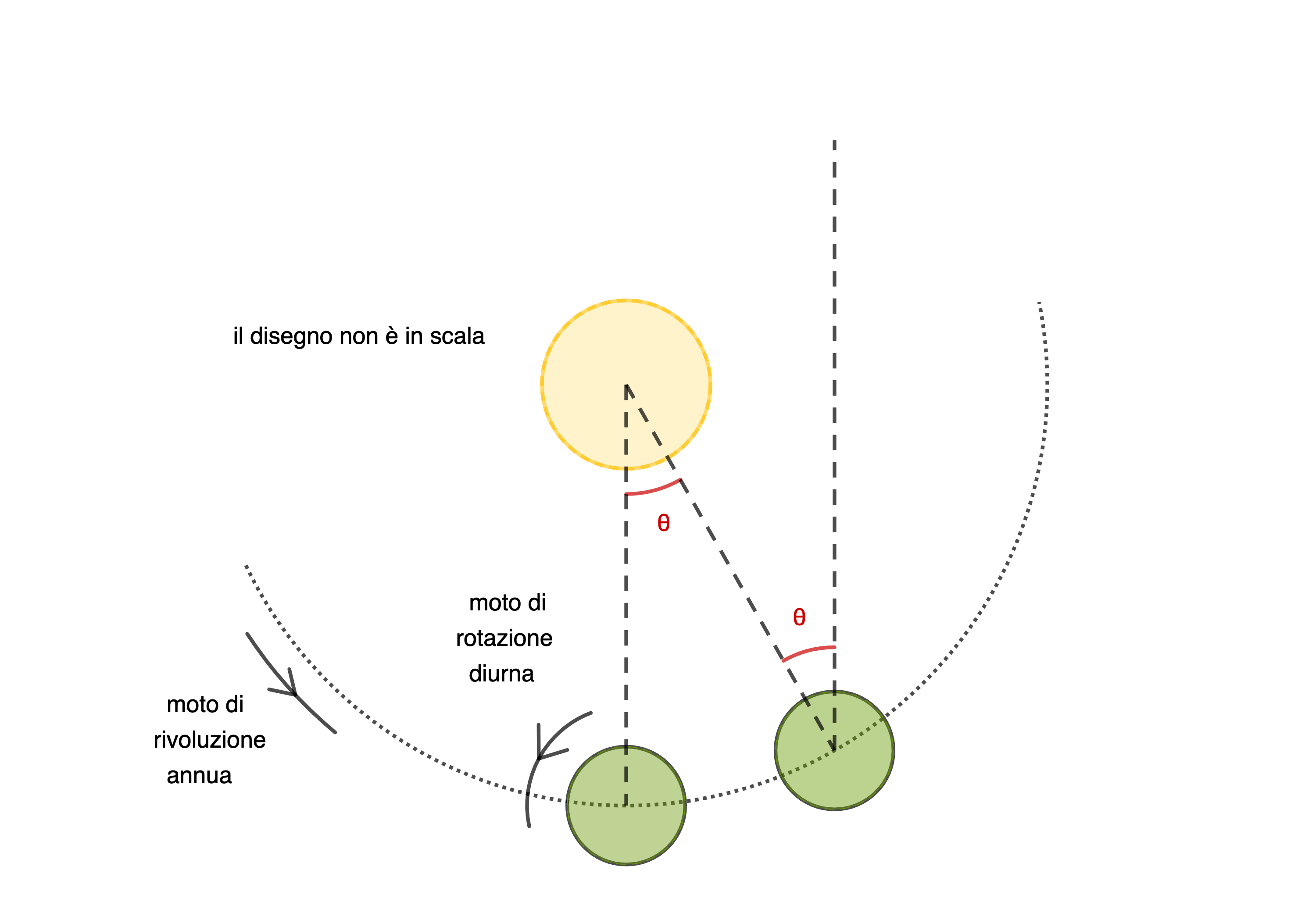
Il giorno siderale è il tempo impiegato dalla Terra per compiere una rotazione completa attorno al proprio asse, o anche l'intervallo di tempo tra due passaggi consecutivi del punto γ dal meridiano del luogo, e la sua durata è di 23h 56m 4s, ovvero dura 3m56s in meno del giorno solare medio. Ciò si spiega nel modo seguente. Dopo 1 giorno siderale il meridiano del luogo sarà nuovamente allineato con le stelle ma non con il Sole perché nel frattempo la Terra avrà percorso un angolo θ ≈ 1° della sua orbita intorno al Sole, nello stesso senso della rotazione per cui, affinché il meridiano del luogo risulti nuovamente allineato con il Sole, è necessario che la Terra compi una rotazione di un angolo θ ≈ 1° attorno al proprio asse, ed il tempo impiegato a compiere tale rotazione è pari a 3m56s (vedasi figura). Ogni giorno, dunque, il Sole ritarda di 3m56s il passaggio in meridiano rispetto al giorno siderale. Questo ritardo giornaliero si accumula e in 1 anno ammonterà ad 1 giorno. La conseguenza è che l’anno siderale sarà pari a 366.25 giorni, 1 giorno in più dell’anno solare.
Il giorno siderale ha inizio nel momento del transito del punto γ al meridiano in direzione sud.
Il Tempo Siderale (t) è definito come l'angolo orario H del Punto γ. A causa della rotazione terrestre, il punto γ sembra ruotare in cielo come un qualunque astro e quindi sorge, transita e tramonta. Il suo angolo orario varierà tra H = 0h quando transita in meridiano, fino a H= 24h al passaggio successivo. Quando il punto γ ha H= 6h, 12h, 18h… saranno, rispettivamente, le ore 6, 12, 18 … di tempo siderale.
Tra l’angolo orario H di una stella, la sua ascensione retta α e il tempo siderale ts esiste la seguente relazione fondamentale:
\( t_s = \alpha + H \)
Se si ha a disposizione un orologio che segni il tempo siderale, ts è noto ed è usato per calcolare l’angolo orario H di un astro di cui si conosca α:
\( H = t_s - \alpha \)
In particolare, quando una stella passa al meridiano in direzione sud si ha H = 0, per cui ts = α.
Questo significa che ad ogni istante passano al meridiano in direzione sud le stelle che hanno ascensione retta pari al tempo siderale in quell’istante.
È evidente che due osservatori posti su due meridiani differenti misureranno due tempi siderali differenti. Ha quindi senso introdurre il concetto di tempo siderale locale.
Siano A, B due località sulla superficie della Terra. Il legame tra i tempi siderali misurati nelle due località (TSL) è espresso dalla seguente formula:
\( TSL_A-TSL_B= \lambda_{BA} \)
dove λBA è la differenza di longitudine tra A e B.
Fissato il meridiano di Greenwich come il meridiano fondamentale, allora si possono scrivere le seguenti due relazioni:
\( TSG = TSL - \lambda \) e \( TSL = TSG + \lambda \)
dove TSG è il tempo siderale misurato al meridiano di Greenwich e λ è la longitudine della località misurata a partire dal meridiano di Greenwich, il cui tempo siderale misurato è TSL.