Il problema dei due corpi
Il problema dei due corpi riguarda il moto di due corpi puntiformi sotto l'azione della legge di gravitazione universale di Newton e che quindi sono in orbita l'uno intorno all'altro.
Per determinare il moto dei due corpi, ovvero risolvere il problema dei due corpi, bisogna trovare l'equazione vettoriale del moto reciproco.
In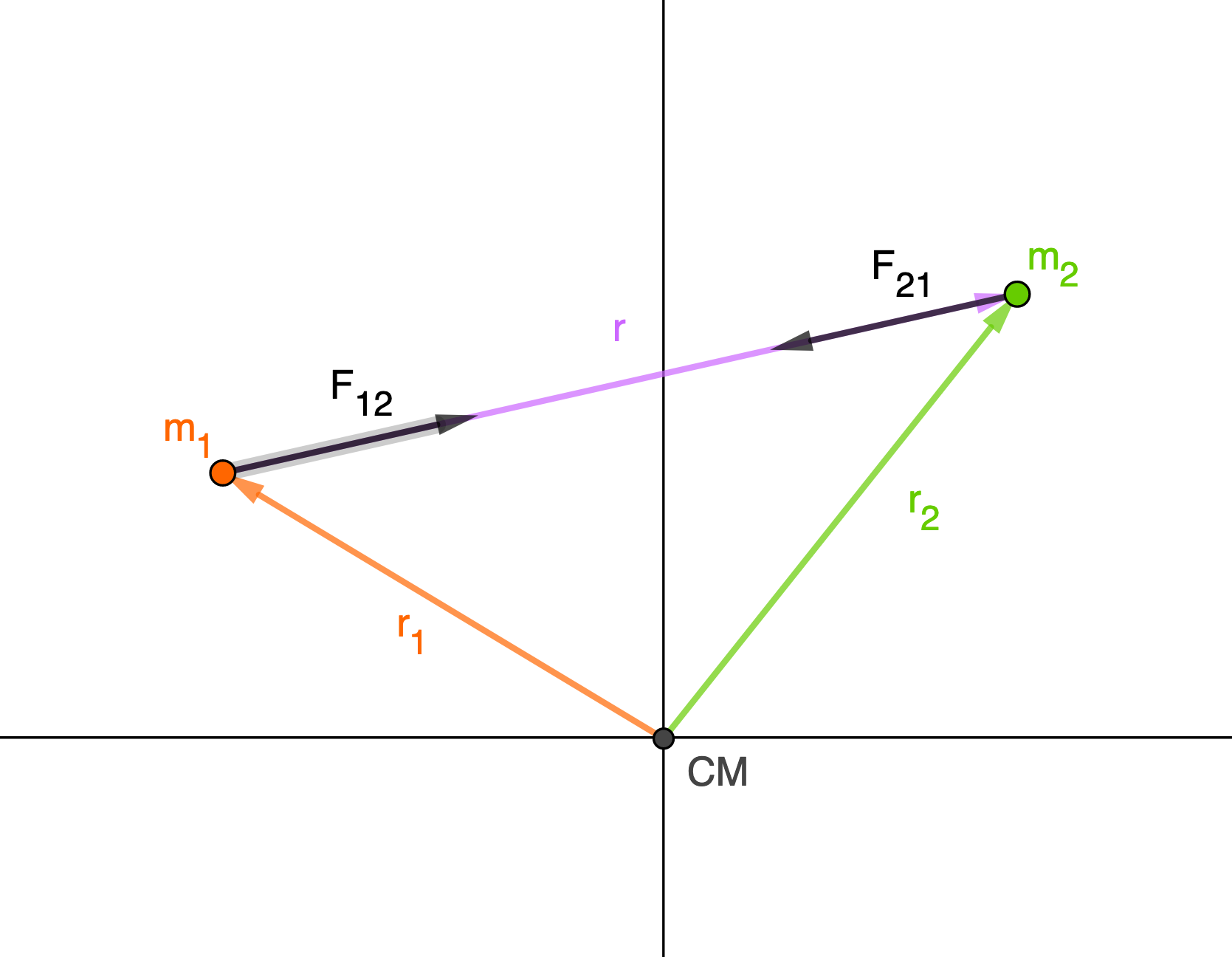
iziamo ponendoci nel sistema di riferimento che ha origine nel centro di massa. Dati due corpi di massa \( m_1 \) e \(m_2\), definiamo \( \vec{r_1} \) il vettore che collega il centro di massa del sistema a \( m_1 \) e \( \vec{r_2} \)
il vettore che collega il centro di massa del sistema a \( m_2 \).
Per definizione, la posizione del centro di massa è \( \vec{R}=\frac{m_1 \vec{r_1} + m_2 \vec{r_2}}{m_1+m_2} \), ma poiché in questo sistema di riferimento coincide con l'origine, si ha \(R = 0\) e quindi: \( \frac{m_1 \vec{r_1} + m_2 \vec{r_2}}{m_1+m_2} = 0 \).
Ora definiamo le seguenti quantità: \( M = m_1 + m_2 \) e \( \mu = \frac{m_1 m_2}{m_1+m_2}=\frac{m_1 m_2}{M} \) dove \( \mu \) è detta massa ridotta.
Il vettore spostamento da \( m_1 \) a \(m_2\) è : \( \vec{r} = \vec{r_2}-\vec{r_1} \). Per
risolvere il problema dei due corpi dobbiamo trovare la dipendenza di \( \vec{r} \) dal tempo.
Quindi, mettendo insieme queste equazioni possiamo scrivere: \( \vec{r_1} = -\frac{m_2}{M}\vec{r} \) e \( \vec{r_2} = \frac{m_1}{M}\vec{r} \).
Ma i due corpi sono soggetti alla reciproca forza di interazione gravitazionale, quindi le equazioni del moto sono rispettivamente:
\( F_{12}= m_1 \vec{\ddot{r_1}} = \frac{Gm_1m_2}{r^2} \hat{r} \) e \( F_{21}= m_2 \vec{\ddot{r_2}} = - \frac{Gm_1m_2}{r^2} \hat{r} \)
dove \( \vec{\ddot{r_1}} \) e \( \vec{\ddot{r_2}} \) sono i vettori accelerazione dei due corpi (l'accelerazione è la derivata seconda del vettore posizione: \( \vec{a} = \frac{d^2 \vec{r}}{dt^2} = \vec{\ddot{r}} \)), mentre \( \hat{r} \) è il versore (vettore di modulo 1) diretto lungo la direzione di \( \vec{r} \).
Calcolando le accelerazioni si ha: \( \vec{\ddot{r_1}} = -\frac{m_2}{M}\vec{\ddot{r}} \) e \( \vec{\ddot{r_2}} = \frac{m_1}{M}\vec{\ddot{r}} \).
Inserendo queste equazioni nelle equazioni del moto si ha: \( -m_1 \frac{m_2}{M}\vec{\ddot{r}} = \frac{Gm_1m_2}{r^2} \hat{r} \Rightarrow \vec{\ddot{r}} =- \frac{GM}{r^2} \hat{r} \) e \( m_2 \frac{m_1}{M}\vec{\ddot{r}} = - \frac{GM}{r^2} \hat{r} \Rightarrow \vec{\ddot{r}} =- \frac{GM}{r^2} \hat{r} \)
ovvero la dipendenza di \( \vec{r} \) dal tempo \( t\) si ottiene risolvendo l'equazione differenziale: \( \vec{\ddot{r}} =- \frac{GM}{r^2} \hat{r} \).
Moltiplicando entrambi i membri per la massa ridotta si ottiene: \( \mu \vec{\ddot{r}} =- \frac{Gm_1m_2}{r^2} \hat{r} \)
Il problema dei due corpi si è quindi ridotto al problema ad un solo corpo. Dall'equazione precedente si conclude che il moto di \( m_1 \) e \(m_2\) intorno al comune centro di massa è del tutto equivalente a quello di una particella di massa pari alla massa ridotta del sistema e soggetta ad una forza \( F = \frac{Gm_1m_2}{r^2}\) che ruota intorno ad un’altra particella di massa pari alla massa totale del sistema ferma nell’origine di un riferimento inerziale.
Determinazione della massa delle componenti di un sistema binario
Per calcolare la massa delle componenti di un sistema binario si può applicare la terza legge di Keplero: \( \frac{P^2}{a^3} = \frac{4 \pi^2}{G(m_1+m_2)} \).
Se le masse delle due componenti sono molto differenti, ovvero un corpo è molto più massiccio dell'altro (ad esempio \( m_1 \ll m_2 \)), l'equazione diventa \( \frac{P^2}{a^3} = \frac{4 \pi^2}{Gm_2} \) e quindi, conoscendo i parametri orbitali dell'orbita di m1 intorno a m2, ovvero il semiasse maggiore "a" e il periodo "P" (che si ricavano dalle osservazione), si deriva la massa del corpo più massiccio.
Se invece le due masse sono simili, si aggiunge una seconda equazione che tiene conto del fatto che i due corpi orbitano intorno al centro di massa del sistema: \( \frac{m_1}{m_2} = \frac{a_2}{a_1} \) dove a1 e a2 sono i semiasse maggiori delle orbite dei due corpi intorno al centro di massa e \( a = a_1 + a_2 \).