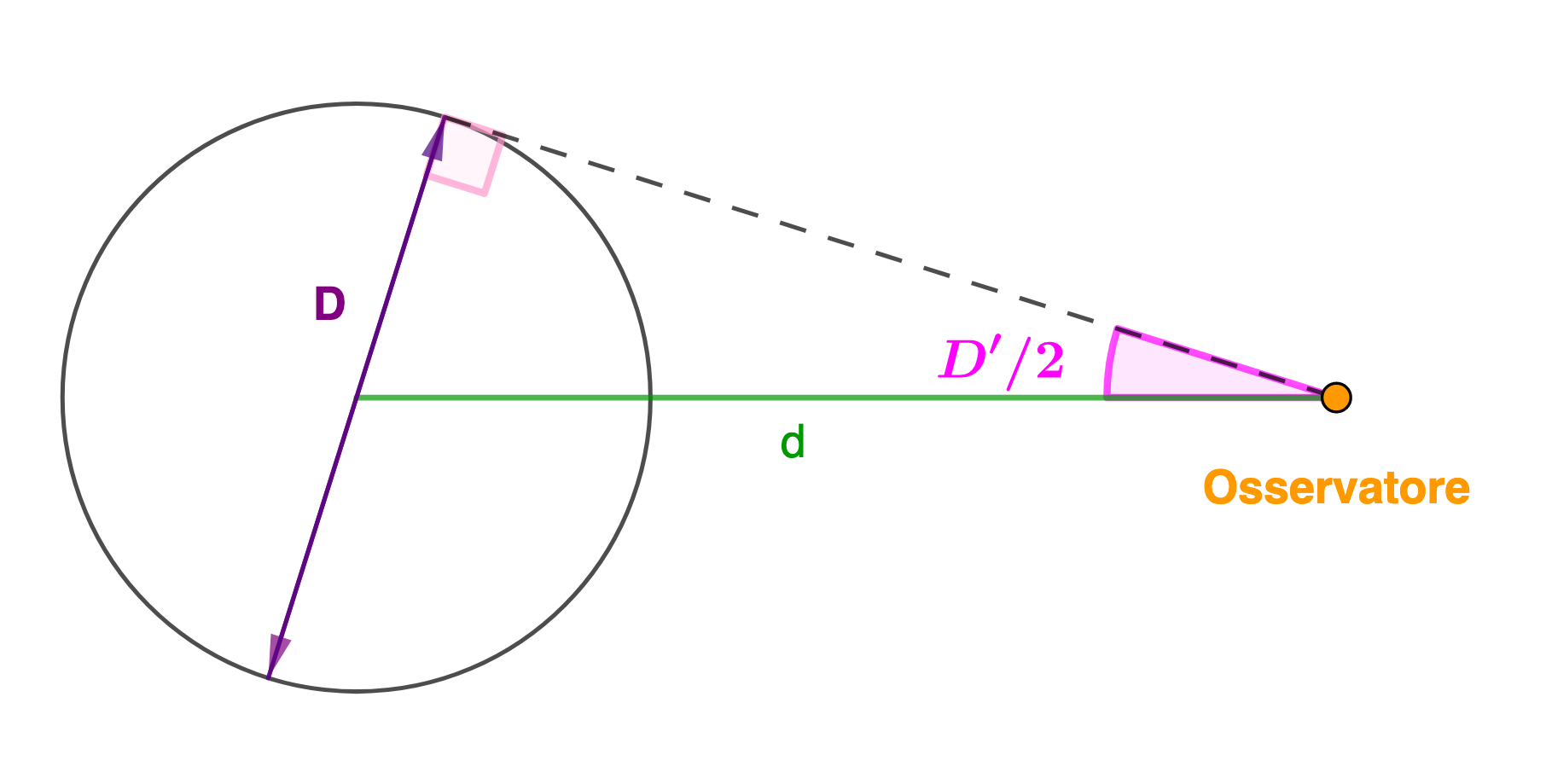
Parallasse
Parallasse annua
Si definisce Parallasse Annua (π) di una stella la metà del suo spostamento apparente (rispetto a stelle molto più lontane) causato dal moto di rivoluzione della Terra intorno al Sole. Poiché l'unità astronomica (la distanza Terra-Sole) è molto piccola rispetto alla distanza delle stelle, anche l’angolo π è molto piccolo e risulta sempre minore di 1" (1" = 1°/3600).
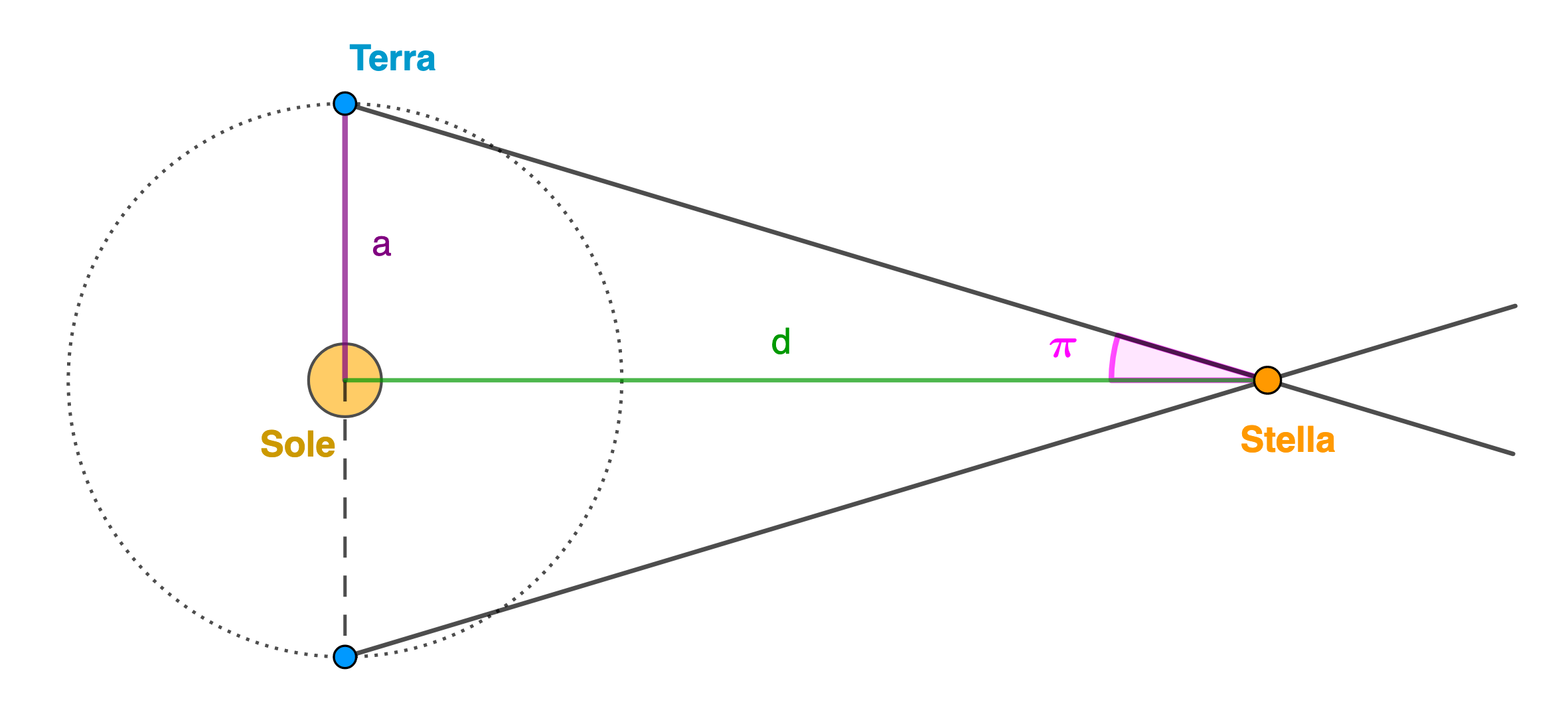Solo nel 1838 F. W. Bessel fu in grado di misurare la prima parallasse stellare: 61 Cygni mostra una parallasse di 0.293", un angolo che equivale alle dimensioni apparenti di una moneta da 1€ vista da una distanza di 16 km.
Le osservazioni da Terra permettono misure di distanza fino ~100 pc. Il satellite Hipparcos ha esteso le misure di distanza fino a circa 1000 pc. Il satellite GAIA, lanciato il 19/12/2013, ha permesso misure estremamente accurate fino a circa 10000 pc.
Si definisce Parsec (pc) la distanza dalla quale 1 UA sottende un angolo di 1" (1 arcsec).
Poiché \( a = d \cdot \tan{\pi} \) ricaviamo che 1 parsec = 206265 UA = 30857 · 109 km
La distanza di una stella in pc è pari all’inverso della sua parallasse annua in secondi d’arco: \( d = \frac{1}{\pi} \) (per esempio se π = 0".04, segue d = 25 pc).
Un Anno Luce (al) è la distanza che la luce percorre nel vuoto in un anno giuliano (= 365.25 g):
1 anno luce = (365.25 · 24 · 60 · 60 · 299792) = 9461 · 109 km = 63240 UA
1 pc = 3.261 anni luce
Dimensioni angolari di una sorgente estesa
Consideriamo una sorgente estesa di diametro "D", osservata da una distanza "d" con D << d. Detto D' il diametro angolare della sorgente estesa vale la relazione:
\( \frac{D}{2} = d \cdot \tan{\frac{D'}{2}} \)
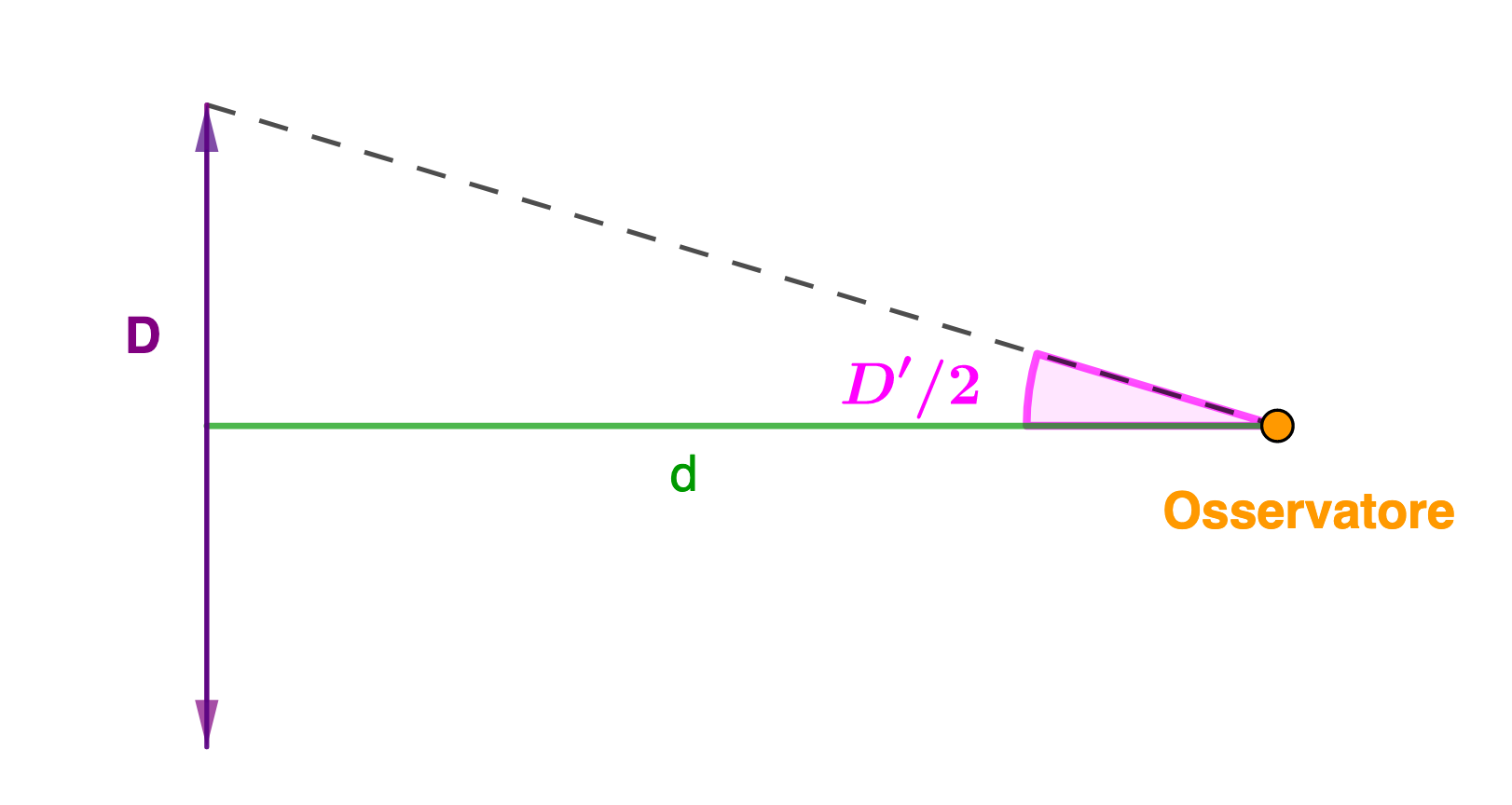
Nella quasi totalità dei casi astronomici si può utilizzare l’approssimazione:
\( D = d \cdot \tan{D'} \)
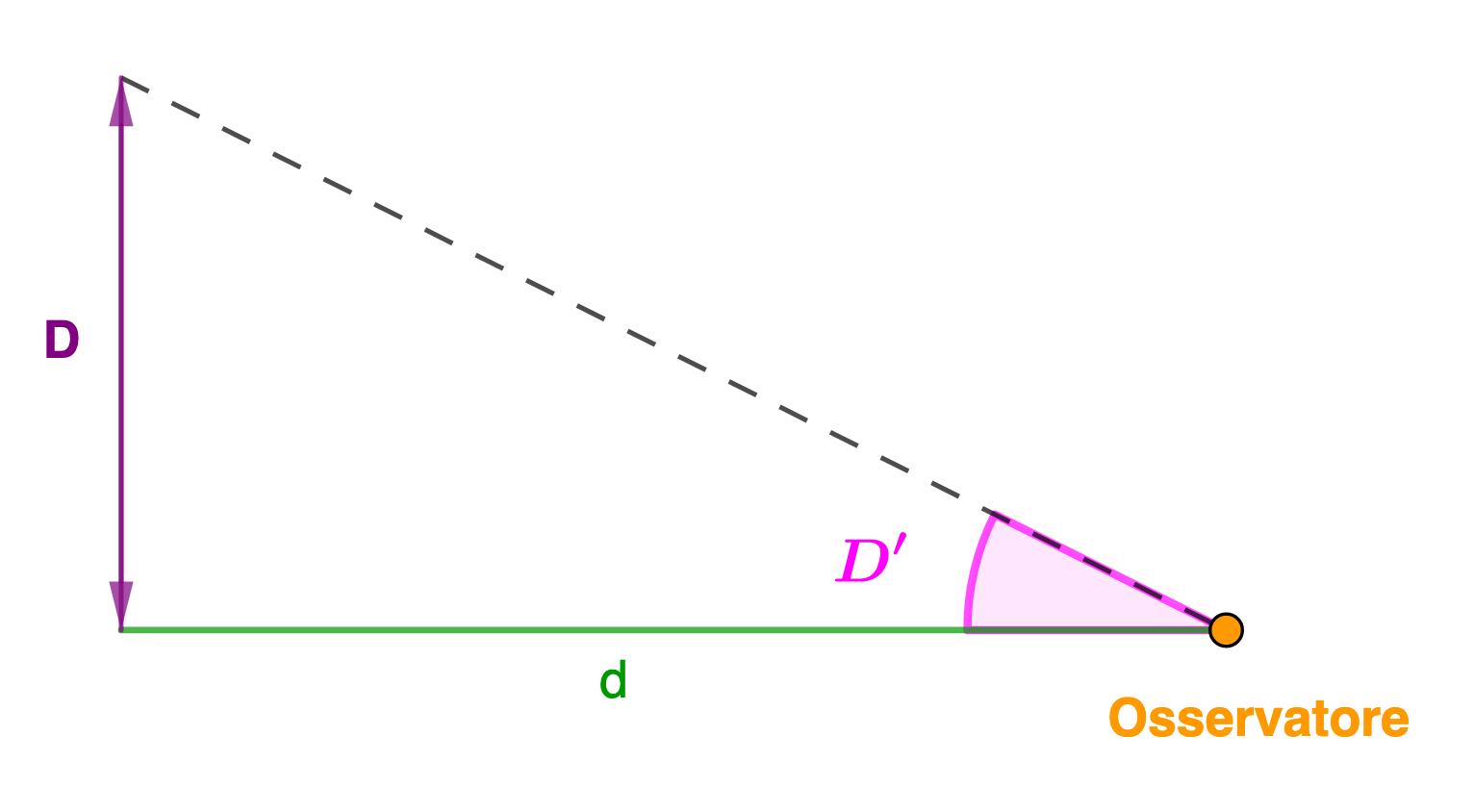
\( D = d \cdot \frac{D'}{206265} \)
con D' espresso in arcosecondi.
Se la dimensione D non è trascurabile rispetto alla distanza d, valgono invece le relazioni:
\( \frac{D}{2} =d \cdot \sin{\frac{D'}{2}} \)
