Telescopi
Introduzione

All’inizio del 1600 in Olanda erano stati sviluppati i primi cannocchiali utilizzati soprattutto nella marina. Questi cannocchiali, con un opportuno sistema ottico di lenti da occhiale, permettevano di ottenere immagini ingrandite di oggetti a distanza.
Questa invenzione si diffuse rapidamente fino alle orecchie di Galilei che, mentre insegnava all’Università di Padova, si propose di svilupparla ulteriormente e di costruire un proprio cannocchiale potenziato. Puntandolo verso il cielo, siamo all’inizio
del 1610, Galilei fece le sue prime grandi scoperte nel cosmo, dando il via alla cosiddetta astronomia moderna. Si diede il via allo sviluppo dei cosiddetti telescopi rifrattori.

Qualche anno dopo Newton costruì un telescopio che non utilizzava lenti ma bensì uno specchio. La luce proveniente dallo spazio non veniva focalizzata attraverso un sistema di lenti, ma attraverso la riflessione su uno specchio a curvatura sferica. I raggi di luce convergenti e riflessi dallo specchio primario vengono intercettati da un secondo specchio piano e portati verso l’esterno del tubo ottico dove l’osservatore può mettere il suo occhio. Nascono così i cosiddetti telescopi riflettori.
Caratteristiche del telescopio
Oltre alla possibilità di poter ingrandire l’immagine di un oggetto, una caratteristica fondamentale del telescopio è il poter raccogliere una quantità di luce maggiore rispetto a quella che può raccogliere l’occhio umano. Da questa considerazione si comprende come l’elemento principale di un telescopio è il cosiddetto obiettivo, ovvero le dimensioni della prima lente nei telescopi rifrattori, oppure le dimensioni dello specchio primario nei telescopi riflettori. La combinazione poi con gli altri elementi ottici definisce le prestazioni complessive di un telescopio. Quali sono quindi le caratteristiche principali da ricercare in un telescopio?
- Quantità di luce raccolta. Abbiamo visto come maggiore è il diametro, maggiore è la quantità di luce raccolta. Se definiamo con \(F\) quest’ultima quantità, essa è direttamente proporzionale alla superficie dell’oggetto di raccolta, ovvero è direttamente proporzionale al quadrato del diametro \(D\) dell’obiettivo: \(F=D^2\). Ad esempio un telescopio con obiettivo di diametro doppio rispetto ad un altro avrà una quantità di luce raccolta maggiore di quattro volte.
Esempio: Quanta più luce riceve un telescopio riflettore con uno specchio primario da 1 m, rispetto al telescopio di Newton che aveva uno specchio da 15 cm? Abbiamo visto che la quantità di luce raccolta è direttamente proporzionale alla superficie dello specchio. Calcolando la superficie dei due specchi (superficie di un cerchio) con diametri 15 cm e 1 m si ottiene che quello da 1 m riceve una quantità di luce 44 volte maggiore.
- Potere risolutivo. Il potere risolutivo teorico (inteso come massima prestazione ottenibile dallo strumento) è la capacità di un telescopio di separare due oggetti che ad occhio sembrano essere uno solo. Un esempio
è quello delle stelle Mizar e Alcor (distanti poco più di 10’ nella costellazione dell’Orsa Maggiore) che un buon occhio e con buone condizioni osservative già vede come due oggetti singoli, ma utilizzando un telescopio ci si accorge che sia Mizar
che Alcor sono loro stessi ognuno un sistema binario. Il potere risolutivo ha come dimensione il secondo d’arco o il radiante essendo la misura di un angolo, se questo angolo è piccolo, maggiore sarà il potere risolutivo e migliore è il dettaglio
dell’immagine (come la separazione di due stelle molto vicine). Il valore della separazione angolare \(\alpha\) di uno strumento è inversamente proporzionale al diametro \(D\) (in millimetri) dell’obiettivo e direttamente proporzionale alla lunghezza
d'onda \(\lambda\) (in millimetri) di osservazione secondo la formula: \( \alpha \mbox{ [rad]} = 1.22 \frac{\lambda}{D} \) oppure \( \alpha \mbox{ ['']} = 1.22 \frac{\lambda}{D} \cdot 206265\) (perché 1 radiante = 57° 17' 45''
= 206265''). Questo potere risolutivo teorico non dipende da nessun altro fattore, mentre quello effettivo sul piano focale (cioè quello effettivamente osservato) dipenderà dalla focale del sistema ottico (lo vedremo in seguito).
Inoltre, nota la distanza \(d\) di un corpo esteso, la dimensione \(P\) del più piccolo particolare del corpo che risulta distinguibile si calcola come: \( P = d \cdot \tan{ \alpha} \).

Esempio: Quanto è il potere risolutivo di un telescopio che osserva nel visibile (λ = 5500 Å = 5.5 · 10-4 mm) con uno specchio primario da 1 m? Abbiamo visto che il potere risolutivo si ottiene dalla formula: \( \alpha \mbox{ ['']} = 1.22 \frac{\lambda}{D\mbox{ [mm]}} \cdot 206265\). Nel caso di un telescopio da 1 m che osserva nel visibile il potere risolutivo sarà di 0.14” (secondi d’arco). Quindi, ad esempio, potremmo dalla Terra distinguere oggetti con 260 m di diametro sulla superficie della Luna.
In realtà il seeing (insieme di fenomeni dovuti all'atmosfera che peggiorano le immagini) impedisce, di norma, di raggiungere il valore teorico di \(\alpha\) e "stabilisce" il potere risolutivo effettivo di un telescopio. Per gran parte dei siti osservativi il seeing vale ~ 1" (pari al potere risolutivo di un obiettivo di 14 cm) che permette di distinguere sulla superficie della Luna solo oggetti con diametro di almeno 1.88 km. La nostra atmosfera introduce quindi delle severe limitazioni al potere risolutivo dei telescopi di grandi dimensioni, ma non alla loro capacità di raccogliere grandi quantità di radiazione. Gli astronomi cercano di limitare gli effetti del seeing con un’opportuna scelta dei luoghi di osservazione o con osservazioni dallo spazio.
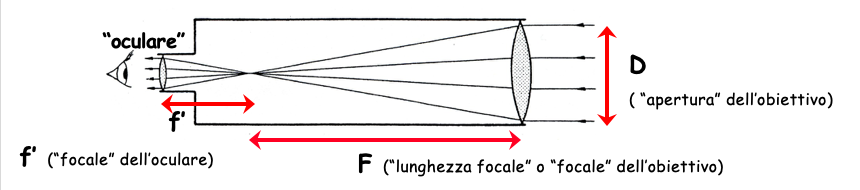
- La lunghezza focale. La lunghezza focale \(F\) rappresenta la distanza del punto di fuoco dell’immagine (distanza del piano focale) dall’obiettivo. In generale nelle caratteristiche di un telescopio (ad esempio nei cataloghi di acquisto dei telescopi si fa riferimento ad un rapporto focale nella forma \(f/n\) - in cui \(n\) è il valore del rapporto focale - o espresso in mm) viene dato il cosiddetto rapporto focale \(f\), dato dal rapporto della lunghezza focale \(F\) e del diametro \(D\) dell’obiettivo: \(f=\frac{F}{D}\). Se il rapporto focale \(f/n\) ha \(n\) piccolo avremo un campo di vista maggiore (con una minore risoluzione spaziale) ed una maggiore luminosità dello strumento (inteso come quantità di luce raccolta per unità di superficie). Al contrario con un rapporto focale \(f/n\) con \(n\) grande si ha un campo di vista più ristretto (maggiore risoluzione spaziale) ma una luminosità dello strumento minore (la stessa quantità di luce viene suddivisa su un’area maggiore).
Esempio: Si ha un telescopio con uno specchio primario da 40 cm e con un rapporto focale \(f/10\). Calcolare la sua lunghezza focale in mm? Abbiamo visto che il rapporto focale \(f\) è dato dalla formula \(\frac{F}{D}\), per cui la lunghezza focale \(F\) sarà dato da \(f \cdot D\), cioè \(400 \cdot 10 = 4000\) mm.
- Scala sul piano focale. Spesso per capire la vera risoluzione spaziale di un telescopio si introduce il concetto di scala sul piano focale FPS. Essa rappresenta la quantità di angolo di cielo osservato in secondi d’arco per ogni millimetro sul piano focale, di conseguenza la sua dimensione sarà “/mm. Prendendo una lente ed utilizzando l’ottica geometrica (qui evito i calcoli) si ottiene che la scala sul piano focale può essere calcolata attraverso la formula \(\mbox{FPS}=\frac{206265}{F}\), dove 206265 rappresenta il numero di secondi d’arco in un radiante ed \(F\) è la lunghezza focale del telescopio.
Esempio: Riprendendo il telescopio dell’esempio precedente quale è la sua scala sul piano focale? Abbiamo visto che il telescopio da 40 cm di specchio ed un rapporto focale di \(f/10\) ha una lunghezza focale \(F\) di 4000 mm. Andando a sostituire questo valore al denominatore della formula della scala si ottiene \(\mbox{FPS}=\frac{206265}{4000}=51.57 \mbox{ ''/mm}\). Per fare un confronto, prendiamo il Telescopio Nazionale Galileo, che ha uno specchio primario di 3.58 m ed un rapporto focale \(f/11\), dai calcoli otterremo una FPS di circa 5.2 “/mm. Questo vuol dire che, pur avendo un rapporto focale pressoché uguale, un rapporto nel diametro dello specchio di dieci volte, migliora di dieci volte circa la risoluzione sul piano focale espressa in “/mm (è quello che avevamo visto in paragrafo 2).
- Scala sulla CCD e campo di vista. Lo scopo finale di un astronomo è quello di acquisire una immagine che gli permetta di studiare l’oggetto celeste di interesse con la migliore risoluzione possibile (pensate alla zona centrale molto densa di stelle in un ammasso globulare) ma che sia ben compreso interamente nell’immagine (pensate alle osservazioni di un'intera galassia). Le immagini, nella banda ottica, vengono acquisite grazie all’utilizzo delle CCD (Charged Coupled Device) che raccolgono la luce sul piano focale del telescopio, la trasformano in carica elettrica ovvero in un segnale analogico (attraverso l’effetto fotoelettrico di un materiale sensibile come il silicio) ed attraverso un convertitore da segnale analogico a digitale (cioè l’immagine bidimensionale, similmente come avviene per le fotocamere dei telefonini). Due caratteristiche importanti di una CCD sono il numero di pixel a disposizione e la loro dimensione. In questo contesto ci sono svariate possibilità di formato di una CCD, ad immagine quadrata (512x512 pixel, 1024x1024 pixel, 4096x4096… 16 megapixel… vi ricorda qualcosa?) o rettangolare con dimensioni dei pixel che sono dell’ordine dei micron. Per quanto riguarda la scala sulla CCD, abbiamo visto che si calcola la scala sul piano focale FPS in “/mm, ora visto che i pixel sono dati in micron basta fare l’opportuna trasformazione dei millimetri. Si ottiene così la scala PS determinata in “/pixel. Se moltiplichiamo il valore di questa scala del singolo pixel per il numero dei pixel su ogni lato otteniamo il campo di vista osservato FOV dalla CCD.

Esempio: Abbiamo un telescopio da 80 cm con un rapporto focale \(f/8\). Al piano focale è stata montata una CCD con un formato 512x512 pixel ognuno con una dimensione di 20 micron. Possiamo con questa strumentazione osservare in un'unica immagine l’ammasso globulare M3 che ha un diametro apparente di 7’?
- L’oculare. Nei telescopi amatoriali per poter osservare “ad occhio” un oggetto celeste con il proprio telescopio si possono utilizzare oculari con differenti lunghezze focali a seconda dell’oggetto celeste (con dimensioni angolari differenti: pianeti, Luna, galassie, ammassi globulari). Come scegliere il giusto oculare per una osservazione ottimale? Si utilizza una formula che mette in relazione la dimensione della pupilla di uscita dell’oculare \(L\), la lunghezza focale del telescopio \(F\), il diametro dell’obiettivo del telescopio \(D\) e la lunghezza focale dell’oculare \(f’\): \(L=D \cdot \frac{f'}{F} \). Se facciamo il rapporto tra la lunghezza focale del telescopio e la lunghezza focale dell’oculare otterremo l’ingrandimento \(I\), ovvero \(I= \frac{F}{f'}\). Se quindi abbiamo un oggetto celeste di cui conosciamo il suo diametro angolare \(\alpha\), noi lo vedremo “ingrandito” nella misura in cui il suo diametro angolare osservato \(\alpha_1\) sarà dato dalla moltiplicazione dell’ingrandimento del sistema \(\alpha_1 = \alpha \cdot I \). Per poter scegliere opportunamente l’oculare adeguato esiste la possibilità di stimare i cosiddetti massimo \(I_max\) e minimo \(I_min\) ingrandimento utile.

Esempio: Abbiamo un telescopio con uno specchio primario di 20 cm ed un rapporto focale \(f/10\). Quale sarebbe il diametro angolare della Luna vista con un oculare la cui pupilla di uscita misura 6 mm? Per poter calcolare l’ingrandimento abbiamo bisogno delle due lunghezze focali (telescopio e oculare). Per prima cosa abbiamo bisogno di sapere la lunghezza focale del telescopio: \(F=D \cdot f= 2000 \mbox{ mm}\). Utilizzando ora la formula vista nel paragrafo 6 opportunamente trasformata, si ha che \(f’=F \cdot \frac{L}{D}=2000 \cdot \frac{6}{200}= 60 \mbox{ mm}\). Ora possiamo calcolare l’ingrandimento dato da \(I=\frac{F}{f’}=\frac{2000}{60}=33.33 \) volte. Sapendo che la Luna ha in cielo una dimensione angolare di 31’, la sua dimensione angolare all’uscita dell’oculare è di \(\alpha_1= \alpha \cdot I= 31’ \cdot 33.33=1033.23’=17.22°\).